Мой знакомый по Греноблю, крупный физик-теоретик и вообще хороший человек Владимир Минеев, прислал мне для ознакомления одну (чужую) статью про классическую электродинамику электрона (КлЭД) (написанную при поддержке американских военных - the Office of Naval Research). Статья старая, 1961-го года и отличается от всего, что я прежде знал, "доказательствами" приемлемости фальстарта в КлЭД.
Фальстартом я называю известное свойство предварительного ускорения, если честно решать уравнение третьего порядка с вредной фигней с тремя точками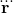 . Частица начинает ускоряться до того, как подействовала сила, что похоже на фальстарт.
. Частица начинает ускоряться до того, как подействовала сила, что похоже на фальстарт.
Из введения: "The previous objections to the theory of radiative reaction are discussed here and are shown to be largely invalid. When this evidence is considered together with the new solutions which are presented here, there no longer appears to be any reason for not accepting these equations as providing an exact classical description of a radiating body."
Тому подтверждение - несколько аналитических и численных расчетов траекторий движения электрона в разных полях, приведенных в статье.
О таком скверном свойстве точных решений, как пред-ускорение, было известно давно, оно нарушало привычное понятие причинности и поэтому большинство физиков не принимало на вооружение уравнение с третьей производной еще и по этой причине (главная причина была - самоускоряющиеся решения). Но автор статьи уверяет, что все ништяк и нечего бояться - решения получаются "физичными", стоит подобрать начальное ускорение, "как надо", и дальше все само пойдет путем, а непричинность маленькая, кто ее заметит? Для известной однородной внешней силы $f(t)$ аналитическое решение уравнения с третьей производной получается таким:
$a(t)=e^{bt}\left[a(0)-\frac{3c^3}{2e^2}\int_{0}^{t}dt'f(t')e^{-bt'}\right],\; b=\frac{3mc^3}{2e^2}.\qquad(1)$
Ну и в общем, если квадратная скобка при больших временах не стремится к нулю, то ускорение экспоненциально нарастает, поэтому начальное ускорение не должно быть любым, а должно быть в точности равно интегралу до бесконечности от будущей силы с некоторым быстро убывающим весом, а не измеренному начальному значению. Такое возможно, если физически ускорение на бесконечности равно нулю: $a(\infty)=0$, что очень трудно реализовать на практике, но давайте допустим. Если соблюсти такое "начальное" условие, то аналитическое решение будет "физичным", но лишь в смысле, что не будет самоускоряющимся:
$a(t)=\frac{3c^3}{2e^2}\int_0^\infty dt f(t'+t)e^{-bt'},\; t\ge 0.\qquad(2)$
Если сделать грубую оценку этого интеграла, то получим
$a(0)\approx f(0)/m,\qquad (3)$
то есть, почти по уравнению Ньютона, что должно успокаивать, в смысле численной разумности величины "начального" значения ускорения, уверяет автор. Интеграл (2) можно считать численно при любой известной внешней силе, что автор статьи предполагает и делает, раз всё будущее у него в руках. Кроме того, и уравнения можно интегрировать численно, не теряя устойчивости, так что траектории получаются "физичными". И я даже допускаю, что такие траектории близки к траекториям, полученным путем решения причинного, но приближенного уравнения, где третья производная заменяется на производную от внешней силы $\dot{\ddot{r}}\to\dot{f}(t)$, правда автор не привел такого сравнения, а мог бы.
Так что единственная нефизичная загвоздка в (2) состоит в необходимости знать будущее для расчета настоящего. И это то, что отталкивало многих исследователей от провозглашения благоденствия в КлЭД. Ведь будущего знать нам не дано. И ведь если частица начинает движение до действия силы, то это против правил. Это как боксер, который бьет своего противника в ухо до сигнала начала боя, рассуждая, что, раз все равно гонг сейчас прозвучит, то хули ждать?
Легко видеть, что дурацкий фальстарт происходит из-за самоускоряющегося решения в (1). Разгонная экспонента $e^{bt}$ перед квадратной скобкой от силы не зависит и всегда больше единицы при $t>0$. Если сила включается строго при $t>0$, то физически $a(0)=0$ и тогда решение получится самоускоряющимся из-за конечности интеграла в (1). Поэтому начальное ускорение "выбирают" не равным нулю при нулевой внешней силе (при нулевом значении интеграла, Фиг. 1). Это и есть пред-ускорение. А бывает и наоборот - сила все еще есть, а ускорения уже нету (Фиг. 2).
Это они - дурацкая разгонная экспонента вместе со специально подобранным нефизичным $a(0)\ne0$, кто делает решение непричинным. Никак не удается до конца победить вредную фигню с тремя точками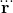 .
.
Из заключения: "Thus, there no longer appears to be any reason for not accepting the equation of motion including the force of radiative reaction, Eq. (1), as an exact equation for a charged point particle within the framework of classical theory."
Я понимаю, что чисто технически (математически), когда все наперед известно, то можно в формулах забегать вперед, в будущее. И я понимаю, что автор статьи не стал бы цепляться за такую "формулировку", если бы теория была бы в духе механики, как всем хотелось до появления такой странной силы радиационного трения. Не от хорошей жизни приходится корячиться с фигней, получившейся в результате самодействия и его переделок. Надо было честно это признать, как многие признали и не зарываться, спасая плохое уравнение. Но наш автор не только не обсудил проблему собственной энергии и голой массы, он вообще движим мотивом продавить идею физической приемлемости фальстарта. Это уже серьезней. Это как маниакальное желание победить любой ценой. Тут кто первый ударит, тот и победит. Короче, если эта идея возобладала, то действовать надо на опережение, иначе проиграешь. Есть даже фильм с таким названием "Бей первым, Фреди". Это понятно и многие, знающие наперед неотвратимое будущее, бьют первыми. Однако такая уверенность в будущем и попытки уйти от судьбы, опережая еще не случившееся, похожа на паранойю. Мы, экстраполируя прошлое, часто можем оценивать вероятности будущих событий и готовиться к ним, но мы-то понимаем, что это оценки, прогнозы, а не точное знание, и у будущего есть варианты. А ну, умный противник глупого боксера, зная повадки последнего, притворится лохом и подловит дурака заранее подготовленным приемом. А ну, вмешается какая нибудь случайность и все пойдет в разнос. Такие просчеты уже бывали, и во избежание попадания впросак выработалась народная мудрость типа "Семь раз отмерь, один раз отрежь", "Не говори "гоп", пока не перепрыгнешь" и "Деньги вперед".
Поэтому попытка протащить в физику сведения из принципиально неизвестного и искомого будущего в качестве основы расчета настоящего, на мой скромный взгляд, предосудительны, как не обоснованные. Уверения, что знать совсем ближайшее будущее в КлЭД принципиально можно, для меня так же не убедительны, как и заверения, что полюс Ландау в КЭД не страшен из-за очень большой "необходимой" энергии, как будто эта энергия не есть простая переменная интегрирования.
P.S. Сид Колеман в своем отчете для других военных тоже утверждает (правда, не доказывает), что непричинное поведение приемлемо. Неужели военным можно продать всё?
Фальстартом я называю известное свойство предварительного ускорения, если честно решать уравнение третьего порядка с вредной фигней с тремя точками
Из введения: "The previous objections to the theory of radiative reaction are discussed here and are shown to be largely invalid. When this evidence is considered together with the new solutions which are presented here, there no longer appears to be any reason for not accepting these equations as providing an exact classical description of a radiating body."
Тому подтверждение - несколько аналитических и численных расчетов траекторий движения электрона в разных полях, приведенных в статье.
О таком скверном свойстве точных решений, как пред-ускорение, было известно давно, оно нарушало привычное понятие причинности и поэтому большинство физиков не принимало на вооружение уравнение с третьей производной еще и по этой причине (главная причина была - самоускоряющиеся решения). Но автор статьи уверяет, что все ништяк и нечего бояться - решения получаются "физичными", стоит подобрать начальное ускорение, "как надо", и дальше все само пойдет путем, а непричинность маленькая, кто ее заметит? Для известной однородной внешней силы $f(t)$ аналитическое решение уравнения с третьей производной получается таким:
$a(t)=e^{bt}\left[a(0)-\frac{3c^3}{2e^2}\int_{0}^{t}dt'f(t')e^{-bt'}\right],\; b=\frac{3mc^3}{2e^2}.\qquad(1)$
Ну и в общем, если квадратная скобка при больших временах не стремится к нулю, то ускорение экспоненциально нарастает, поэтому начальное ускорение не должно быть любым, а должно быть в точности равно интегралу до бесконечности от будущей силы с некоторым быстро убывающим весом, а не измеренному начальному значению. Такое возможно, если физически ускорение на бесконечности равно нулю: $a(\infty)=0$, что очень трудно реализовать на практике, но давайте допустим. Если соблюсти такое "начальное" условие, то аналитическое решение будет "физичным", но лишь в смысле, что не будет самоускоряющимся:
$a(t)=\frac{3c^3}{2e^2}\int_0^\infty dt f(t'+t)e^{-bt'},\; t\ge 0.\qquad(2)$
Если сделать грубую оценку этого интеграла, то получим
$a(0)\approx f(0)/m,\qquad (3)$
то есть, почти по уравнению Ньютона, что должно успокаивать, в смысле численной разумности величины "начального" значения ускорения, уверяет автор. Интеграл (2) можно считать численно при любой известной внешней силе, что автор статьи предполагает и делает, раз всё будущее у него в руках. Кроме того, и уравнения можно интегрировать численно, не теряя устойчивости, так что траектории получаются "физичными". И я даже допускаю, что такие траектории близки к траекториям, полученным путем решения причинного, но приближенного уравнения, где третья производная заменяется на производную от внешней силы $\dot{\ddot{r}}\to\dot{f}(t)$, правда автор не привел такого сравнения, а мог бы.
Так что единственная нефизичная загвоздка в (2) состоит в необходимости знать будущее для расчета настоящего. И это то, что отталкивало многих исследователей от провозглашения благоденствия в КлЭД. Ведь будущего знать нам не дано. И ведь если частица начинает движение до действия силы, то это против правил. Это как боксер, который бьет своего противника в ухо до сигнала начала боя, рассуждая, что, раз все равно гонг сейчас прозвучит, то хули ждать?
Легко видеть, что дурацкий фальстарт происходит из-за самоускоряющегося решения в (1). Разгонная экспонента $e^{bt}$ перед квадратной скобкой от силы не зависит и всегда больше единицы при $t>0$. Если сила включается строго при $t>0$, то физически $a(0)=0$ и тогда решение получится самоускоряющимся из-за конечности интеграла в (1). Поэтому начальное ускорение "выбирают" не равным нулю при нулевой внешней силе (при нулевом значении интеграла, Фиг. 1). Это и есть пред-ускорение. А бывает и наоборот - сила все еще есть, а ускорения уже нету (Фиг. 2).
Это они - дурацкая разгонная экспонента вместе со специально подобранным нефизичным $a(0)\ne0$, кто делает решение непричинным. Никак не удается до конца победить вредную фигню с тремя точками
Из заключения: "Thus, there no longer appears to be any reason for not accepting the equation of motion including the force of radiative reaction, Eq. (1), as an exact equation for a charged point particle within the framework of classical theory."
Я понимаю, что чисто технически (математически), когда все наперед известно, то можно в формулах забегать вперед, в будущее. И я понимаю, что автор статьи не стал бы цепляться за такую "формулировку", если бы теория была бы в духе механики, как всем хотелось до появления такой странной силы радиационного трения. Не от хорошей жизни приходится корячиться с фигней, получившейся в результате самодействия и его переделок. Надо было честно это признать, как многие признали и не зарываться, спасая плохое уравнение. Но наш автор не только не обсудил проблему собственной энергии и голой массы, он вообще движим мотивом продавить идею физической приемлемости фальстарта. Это уже серьезней. Это как маниакальное желание победить любой ценой. Тут кто первый ударит, тот и победит. Короче, если эта идея возобладала, то действовать надо на опережение, иначе проиграешь. Есть даже фильм с таким названием "Бей первым, Фреди". Это понятно и многие, знающие наперед неотвратимое будущее, бьют первыми. Однако такая уверенность в будущем и попытки уйти от судьбы, опережая еще не случившееся, похожа на паранойю. Мы, экстраполируя прошлое, часто можем оценивать вероятности будущих событий и готовиться к ним, но мы-то понимаем, что это оценки, прогнозы, а не точное знание, и у будущего есть варианты. А ну, умный противник глупого боксера, зная повадки последнего, притворится лохом и подловит дурака заранее подготовленным приемом. А ну, вмешается какая нибудь случайность и все пойдет в разнос. Такие просчеты уже бывали, и во избежание попадания впросак выработалась народная мудрость типа "Семь раз отмерь, один раз отрежь", "Не говори "гоп", пока не перепрыгнешь" и "Деньги вперед".
Поэтому попытка протащить в физику сведения из принципиально неизвестного и искомого будущего в качестве основы расчета настоящего, на мой скромный взгляд, предосудительны, как не обоснованные. Уверения, что знать совсем ближайшее будущее в КлЭД принципиально можно, для меня так же не убедительны, как и заверения, что полюс Ландау в КЭД не страшен из-за очень большой "необходимой" энергии, как будто эта энергия не есть простая переменная интегрирования.
P.S. Сид Колеман в своем отчете для других военных тоже утверждает (правда, не доказывает), что непричинное поведение приемлемо. Неужели военным можно продать всё?



Комментариев нет:
Отправить комментарий