Мне тоже немножко повезло (гол в свои ворота)

Гриша описал, как ему повезло родиться в 4-х мерном пространстве, и я, подражая ему, решил тоже обрисовать одну свою удачу.



Собственно, удача эта очень условная и началась с позора: читая лежа блог Любоша Мотла (статья про твистеры), я решил задать ему каверзный вопрос, на который я сам не знал точного ответа. Любош что-то писал про извлечение квадратного корня из вектора, мол, получается спинор. Меня это раззадорило и я задал вопрос, внезапно пришедший мне в голову: чему равны собственные значения проекции орбитального момента электрона в позитрониуме, когда орбитальный момент позитрониума равен единице? (Спинами пренебрегаем). Позитрониум - симметричная по массам система и его полный орбитальный момент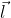 равен сумме орбитальных моментов электрона 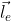и позитрона 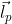(по определению). Если проекция полного момента 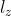пробегает целые значения -1, 0, 1, то проекция момента одной из частиц, например, , казалось бы, пробегает полуцелые значения и ноль: = -1/2, 0, +1/2. То же самое в силу симметрии пробегает и проекция углового момента позитрона. Конечно, такого не может быть, но как дело обстоит на самом деле, я сам сначала не стал разбираться, а переложил это бремя на Любоша. Я подумал, если он такой умный, то пусть сам выкручивается, как не получить 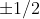в совершенно симметричной ситуации. Это попроще, чем извлекать квадратный корень из вектора. (Надо сказать, что почти все мои дискуссии с Любошем превращаются в отвратительный базар - он начинает орать матом и  объяснять какой я безнадежный придурок. Крайне редко ему удается ответить в масть и без мата. Ну, и ничему правильному он меня еще не научил). Короче, сам он никаких выкладок проводить не стал, а просто голословно заявил, что такого быть не может. Привожу цитату из его ответа, так как она - перл и я его в конце концов засчитал, как отписку, формально оказавшуюся правильной:

"No. If the sum of two angular momenta equals 1, it doesn't mean that both of them are equal, i.e. that both of them have to be 1/2. Nature doesn't obey any egalitarianism of this naive sense. And indeed, the orbital momentum has to be integer which implies that it cannot be 1/2, not even for a single article, so it's guaranteed that the total orbital momentum 1 is shared unequally by the two objects."
 

Дальше пошла грязная брань и обсуждение с другими читателями его блога. Однако, никто так и не предложил удовлетворительного объяснения. Писали о правиле сложения независимых моментов, не имеющем отношения к данному случаю.  

Я, зная с юности, что электрон в атоме всегда находится в смешанном состоянии и не имеет определенных квантовых чисел, но ленясь сделать элементарные выкладки сам и не получив  внятного ответа от других, стал рассуждать так: если я полагаю полный импульс атома нулю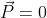 , то зависимость волновой функции от координаты центра масс исчезает и остается зависимость лишь от относительного электрон-позитронного расстояния 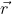. Единственная величина в , которая зависит только от 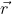это сам орбитальный момент 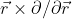, а всякие там градиенты 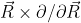зануляются в силу отсутствия зависимости волновой функции 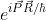от  . Полный импульс системы 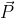идет ведь лишь в виде произведения с координатой центра масс и равенство нулю импульса эквивалентно равенству нулю , умствовал я. Поэтому в данном конкретном случае орбитальный момент одной частицы 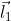 выражается через полный орбитальный момент 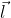: и все, т.е., он является просто операторной функцией "первичного" оператора 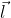, для которого и писаны правила квантования. Ну, а функция целого числа не обязана быть целой.

Так я увлекся размышлениями и потихоньку сам себя переубедил, что в данном конкретном случае орбитальный момент одной частицы в симметричной системе может принимать полуцелые значения. (В этом и был мой главный позор). А убедивши, поторопился полезть с этим в Science 2.0, где затеял еще одну дискуссию. Там тоже не нашлось никого, кто указал бы мне на правильное решение. В итоге, томясь душою и проклиная свои болезни, я поднялся с кровати, сел за стол и проделал вычисления сам. Ну конечно, гадская зависимость от все же осталась, но не в волновой функции, а в операторе 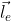, так что оператор углового момента одной частицы никак не сводится к части полного орбитального момента: имеется еще и "флуктуирующее" слагаемое 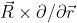(вектор произволен в области волнового пакета атома), причем в электронном моменте оно (слагаемое) одного знака, а в позитронном - противоположного. В сумме обоих моментов "флуктуационные" члены взаимно уничтожаются, а в раздельности - нет, и вот "пророческая" фраза Любоша про обязательное неравенство наполнилась конкретным содержанием. Средние значения проекций действительно не целые, как я и предполагал, но они  - не собственные значения, а средние. Собственных значений оператора вообще нет, так как электрон в атоме находится все время в смешанном состоянии. Я разместил соответствующую заметку в сети, повинился, покаялся и порадовался, что сам справился раньше всех. В этом и есть, собственно, мое везение в данном вопросе. Кстати, Ромa Lee, когда я ему задал эту задачу, не сплоховал и не ударился в правило сложения независимых моментов. Он все точно описал на словах, за исключением одной формулы, но за ошибку это уже не считается - он был на совершенно правильном пути.

По правде говоря, такое безобразие со мной произошло в первый раз. Обычно я не лезу на публику с непроверенными утверждениями. То есть, с неправильными - да, но по своему искреннему заблуждению. А тут я знал наперед, что есть подвох и червячок сомнения меня глодал, но я купился (пусть даже на короткое время) на собственные красивые "умные" рассуждения ("функция оператора") и облажался публично. Будет мне наука.