A recent book by Alexander Unzicker "The Higgs Fake"
considers, in particular, how "particle physicists are fooling
themselves with alleged results, while their convictions are based on
group-think and parroting." It represents a critical point of view and
it is not groundless. I would like to support Alexander Unzicker in his critics. In former times the founding fathers of physics were speaking
of non resolved fundamental problems, which are still not resolved
satisfactorily, but nowadays everything is represented as a
fulfledged building based on some fundamental principles. Let us take,
for example, a citation of W. Pauli, one of most honest physicist of the
last century:
"We will be considered the generation that left behind unsolved such essential problems as the electron self-energy."
I
think the essence is here and avoiding it created just a shaman's
practice where cheating and self-fooling are essential parts. To prove
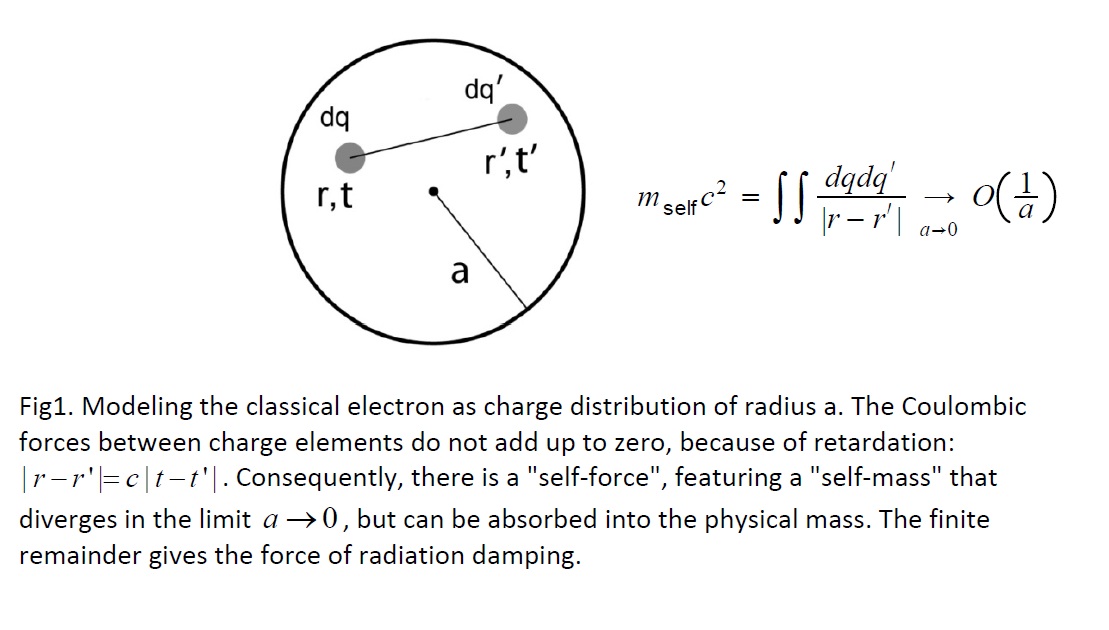
that, let me be more specific and let us consider the electron
electromagnetic mass. This notion had arisen in Classical
Electrodynamics (CED) well before the famous $E=mc^2$ was derived
[1] and it remains an unsolved problem even today (there are still
publications on this subject). We must not confuse it with the
electromagnetic mass defect, though, i.e., with a calculable interaction energy.
The
electromagnetic mass can be thought of as a Coulomb energy of the
electric field surrounding the electron when we calculate the total
field energy. In other words, it is a consequence of the field concept.
This part of the field energy is cut-off dependent and thus can take any
value at your convenience. We all are familiar with the classical
radius of electron $ r_0=e^2/mc^2$, but if we take into account the
electron magnetic field energy too, we will obtain another radius,
closer to the Compton length $ \hbar/mc$. Still, in nature there is no
electron of the classical or any other radius. And normally this part of
the field energy is entirely discarded and what is left is an
interaction energy of charges. Thus, when we calculate a field energy, the electromagnetic mass is just of no use.
Apart
from the total field energy, the electromagnetic mass of a point-like
charge $ m_{em}$ enters the usual "mechanical" equation of a charge
when we decide to insert the charge proper field into the charge
equation of motion in the frame of a self-action ansatz. The latter is
done for the sake of taking into account a weak radiation reaction
force, which must provide the total energy conservation. The motivation -
energy conservation - is understandable, but in a field approach with
$ \mathcal{L}_{int}\propto j\cdot A$, we insert the entire filed $
F_{\mu\nu}$, not just a radiation field $ F_{\mu\nu}^{rad}$, in the
mechanical equation. We do it by analogy with an external force $
F_{\mu\nu}^{ext}$. So, before this our intervention we have a good
"mechanical" equation (I use a non relativistic form)
$ m_e \ddot{ \mathbf{r} }= \mathbf{F}_{ext},\qquad (1)$
which
works almost fine (the near field, whatever it is, easily follows the
charge according to Maxwell equations), and after our noble intervention
it becomes
$ m_e \ddot{ \mathbf{r} }= \mathbf{F}_{ext} - m_{em}\ddot{ \mathbf{r} } + \frac{2e^2}{3c^3}\dot{\ddot{\mathbf{r}}}.\qquad (2)$
that
does not work any more. The corresponding self-force term $ -
m_{em}\ddot{ \mathbf{r} }$ with $ m_{em}\to\infty$ makes it
impossible for a charge to change its state of a uniform motion $ \mathbf{v}
= const$. This is a self-induction force, an extremely strong one. It's
an understandable "physical effect", but first, it is not observed as
infinite, and second, the self-induction force is not a radiation
reaction force in any way, so our approach to describing the radiation
influence via self-action is blatantly wrong. Albeit of an anticipated
sign (and even when made finite and small), it does not help conserve
the total energy. Microsoft Windows would say:
I. e., the term $ - m_{em}\ddot{ \mathbf{r} }$ is not of the right functional dependence. Instead
of recognizing this error, physicists started to search a pretext to
keep to the self-action idea in place. They noticed that discarding the
term $ - m_{em}\ddot{ \mathbf{r} }$ "helps" (we will later see how
it helps), but calling it honestly "discarding" makes fun of physicists.
Discarding is not a calculation. Thus, another brilliant idea was
advanced - an idea of "bare" mass $ m_0 =m_e-m_{em}$ that "absorbs"
$ m_{em}$ (a "mechanism" called later a mass renormalization).
Tricky is Nature, but clever are physicist. In a fresh historical paper Kerson Huang expresses the common attitude to it [2]:
"One notices with great relief that the self‐mass can be absorbed into the physical mass in the equation of motion"
and he writes down an equation, which experimentally follows from nowhere:
$ m_0 \ddot{ \mathbf{r} }= \mathbf{F}_{ext} - m_{em}\ddot{ \mathbf{r} } + \frac{2e^2}{3c^3}\dot{\ddot{\mathbf{r}}}.\qquad (3)$
It
is here where the negative bare mass $ m_0 < 0 $ is introduced in
physics by physicists, introduced exclusively with the purpose to
subtract the harmful electromagnetic mass. This introduction is not
convincing to me. A negative mass makes the particle move to the left
when the force pulls it to the right. We never observed such a silly behavior (like that of a stupid goat) and we never wrote the corresponding equations. We cannot
pretend that (1) describes such a wrong particle in an external field,
but adding its self-induction makes the equation right, as it does
Kerson Huang. It's all the way around: in order to make the wrong
equation (2) closer to the original one (1), we just discard the electromagnetic mass whatever value it takes. Kerson Huang should have written honestly "One notices that the self‐mass ought to be omitted".
As
well, those who refer to a hydrodynamics analogy, present this silly
speculation about arbitrary $ m_0$ and $ m_{em}$ as a typical
calculation, a calculation like in hydrodynamics where everything is
separately measurable, known, and physical. In CED it is not the case. And if the electromagnetic
mass is present already in our phenomenological equation (1), the method
of self-action takes it into account once more which shows again that
such an approach is self-inconsistent. You know, self-induction of a
wire is in fact a completely calculable physical phenomenon occurring
with many interacting charges. Similarly in plasma description we calculate interactions
for dynamics. Interaction is a good concept, but a self-action of an
elementary particle is a bad idea. It describes no internal dynamics by
definition.
If
a bare particle is not observable, we cannot even establish an equation
for it and we cannot pretend that its equation is of the same form as
the Newton equations for physical particles. They, however, say the bare
mass is not observable alone - it always comes in (3) together with the
electromagnetic one: $ m_0 +m_{em}=m_e$. But it is not true
either: equation (1) contains the physical mass $ m_e$ and in
addition, if the external force in (1) contains the omnipresent gravity
force, say, $ m_e g$ for simplicity, the latter does not acquire
any addendum when we add that self-induction force. In reality, we fight
our own invention $ m_{em}$ with help of another one - $
m_0$, but too many people believe in both.
This
is the real truth about mass "renormalization" procedure. We ourselves
introduce the self-mass in our equation and then we remove it. As
nothing remains from it anywhere (the physical mass stays intact), I can
safely say that there is no electromagnetic mass at all, that's my
answer to this question (again, not to confuse with the mass defect due
to interaction). (By the way, renormalization does not work without fail
- there are many non renormalizable theories where bad interaction
terms spoil not only the original equation coefficients, but also
introduce wrong "remainders". Success of renormalization is based on
lucky accidents, see my opus here or here. P. Dirac clearly called it a fluke.)
Those who insist on this “calculation” forget that then there are forces keeping the charge parts together and these forces have their own self-induction and radiation reaction contributions. No, this model needs too many “unknowns”.
Those who insist on this “calculation” forget that then there are forces keeping the charge parts together and these forces have their own self-induction and radiation reaction contributions. No, this model needs too many “unknowns”.
Here
I naively wonder why not from the very beginning to use just the
radiated field instead of the total field to take into account the
"radiation reaction"? Then they might never obtain the harmful jerk term
$ \propto \dot{\ddot{\mathbf{r}}}$, but they do not do it. They stick
to the self-action patched with the "bare mass mechanism" and they hope
that the jerk "remainder" of self-action will correctly describe the radiation reaction. Let us see.
So,
after shamefully camouflaging discarding silly $ m_{em}\ddot{
\mathbf{r} }$, they are left with the jerk $
\frac{2e^2}{3c^3}\dot{\ddot{\mathbf{r}}}$ called a "radiation reaction"
force:
$ m_e \ddot{ \mathbf{r} }= \mathbf{F}_{ext} + \frac{2e^2}{3c^3}\dot{\ddot{\mathbf{r}}}.\qquad (4)$
Fortunately,
it is wrong too. I say "fortunately" because it reinforces my previous
statement that the self-action is a wrong idea. This remainder cannot be used as it gives runaway solutions. Not small radiation reaction, but a rapid self-acceleration. Microsoft Windows would say:
I. e., the term $\frac{2e^2}{3c^3}\dot{\ddot{\mathbf{r}}}$ is not of the right functional dependence either. In other words, all terms of self-action force in (2) are wrong. Some textbook authors are even happy that the jerk term does not depend on the charge shape, but I personally think such a force is not physical either - precisely because of this "lucky" feature. This self-action idea was tried and it failed miserably. Period.
(This self-action can be figuratively represented as connecting an amplifier output to its input. It creates a feedback. First the feedback is strongly negative – no reaction to an external signal is possible anymore. After “repairing” this self-action, we get a strong positive feedback. Now we have a self-amplification whatever the external signal value is. No good either.)
A.
Unzicker speaks of a fake and for some readers this may look as an
exaggeration. If you want to see physicists cheating, here is another
bright example. This cheating consists in using $ \dot{\ddot{\mathbf{r}}}$ in their "proof" of energy
conservation [3], as if the corresponding equation (4) had physically
reasonable quasi-periodical solutions. But it doesn't! Runaway solutions
are not quasi-periodical and are not physical at all, so the proof is
just a deception. (They multiply $ \dot{\ddot{\mathbf{r}}}$ by $ \dot{\mathbf{r}}$
and integrate it by parts to "show" that on average it is a radiation
power.) If they insist on using quasi-periodic solutions in their proof, these solutions do not belong to Eq. (4). (A "jerky" equation like (4) does not even have any physical Lagrangian to be directly derived from!)
As a matter of fact, after cheating with the "proof",
this harmful jerk term is also (quietly) abandoned in favor of some
small force term used in practice instead. This small term is $
\frac{2e^2}{3m_e c^3}\dot{\mathbf{F}}_{ext}$ (or alike):
Equation
(5) is much better, but here again, I notice cheating once more because
they represent it as a "derivation" from (4). Now cheating consists in replacing $\dot{\ddot{\mathbf{r}}} $ with $ \dot{\mathbf{F}}_{ext}$ as if we solved
(4) by iterations (perturbation method). However, in the true iterative
procedure we obtain a given function of time $
\dot{\mathbf{F}}_{ext}^{(0)}(t)=\dot{\mathbf{F}}_{ext}\left(\mathbf{r}^{(0)}(t),\mathbf{v}^{(0)}(t)\right)$
on the right-hand side rather than a term $
\dot{\mathbf{F}}_{ext}$ expressed via unknown dynamical variables $ \mathbf{r}$ and $ \mathbf{v}$. For example, in an oscillator equation
the
first perturbative term $ \dot{F}_{ext}^{(0)}(t)\propto
\dot{y}^{(0)}(t)$ is a known external periodic (resonance!) driving
force whereas the replacement term $ \dot{F}_{ext}\propto \dot{y}$
is unknown damping force (kind of a friction):
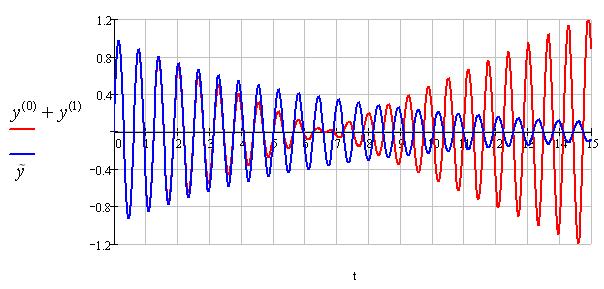
$ \ddot{\tilde{y}}+ \gamma\,\dot{\tilde{y}}+ \omega^2 \tilde{y}= 0,\quad \gamma=\frac{2e^2\omega^2}{3mc^3}.\qquad (7)$
A perturbative solution to (6) $ y\approx y^{(0)} + y^{(1)}$ (a red line in Fig. 2)
Fig. 2.
is
different from a damped oscillator solution $ \tilde{y}$ (a blue
line in Fig. 2). Solution to a damped oscillator equation is non linear
in $ \gamma$, non linear in a quite certain manner. It is not a self-action, but an interaction with something else. This difference
in equations is qualitative (conceptual) and it is quantitatively
important in case of a strong radiation reaction force and/or when
$ t\to\infty$ (I used in this example $ y^{(0)}=\sin\omega t$
with $ \omega=10$ and $ \gamma=0.3$). I conclude therefore
that a damped oscillator equation (7) is not a perturbative version of
(6), but is another guesswork result tried and left finally in practice
because of its physically more reasonable (although still approximate) behavior. Similarly, equation (5) is not a perturbative version of (4),
but another (imperceptible) equation replacement [3], [4]. Of course,
there is no and may not be any proof that perturbative series for (4)
converge to solutions of (5). The term $\frac{2e^2}{3m_e c^3}\dot{\mathbf{F}}_{ext}(\mathbf{r},\dot{\mathbf{r}})$ is a third functional dependence tried for description of the radiation reaction force.
Hence, researchers have been trying to derive equations
describing the radiation reaction force correctly, but they've failed.
For practical (engineering) purposes they constructed (found by trying
different functions) approximate equations like (5) that do not provide
the exact energy conservation and do not follow from "principles" (no
Lagrangian, no Noether theorem, etc.). Factually the field approach has
been "repaired" several times with anti-field guesswork, if you like.
Anyway, we may not represent it as a continuous implementation of
principles because it isn't so.
Guessing
equations, of course, is not forbidden, on the contrary, but this story
shows how far away we have gone from the original idea of self-action.
It would not be such a harmful route if the smart mainstream guys did
not raise every step of this zigzag guesswork into "the guiding
principles" - relativistic and gauge invariance, restricting,
according to the mainstream opinion, the form of interaction to $
j\cdot A$. Nowadays too few researchers see these steps as a severe lack
of basic understanding of what is going on. On the contrary, the
mainstream ideology consists in dealing with the same wrong self-action
mechanism patched with the same discarding prescription
("renormalization"), etc., but accompanied also with anthems to these
"guiding principles" and to their inventors. I do not buy it. I
understand the people's desire to look smart - they grasped principles
of Nature, but they look silly to me instead.
Indeed, let us for a moment look at Eq. (5) as at an exact
equation containing the desirable radiation reaction correctly. We see,
such an equation exists (at least, we admit its existence), it does not
contain any non physical stuff like $ m_{em}$ and $ m_0 $,
and together with Maxwell equations it works fine. Then why not to
obtain (5) directly from (1) and from another physical concept different
from a wrong self-action idea patched with several forced replacements
of equations? Why do we present our silly way as a right and unique?
Relativistic and gauge invariance, as equation properties, are borrowed from inexact CED equations, hence as "principles" they may not guarantee the correctness of theory completion. Relativistic and gauge invariance (equation properties) must be
preserved, nobody argues, but making them "guiding principles" only
leads to catastrophes, so (5) it is not a triumph of "principles", but a
lucky result of our difficult guesswork done against the misguiding
principles. Principles do no think for us researchers. Thinking is our
duty. Factually we need in (1) a small force like that in (5), but our
derivation gives (2). What we then do is a lumbering justification of
replacements of automatically obtained bad functions with creatively
constructed better ones. Although equations like (5) work satisfactorily
in some range of forces, the lack of mechanical equation with exact
radiation reaction force in CED shows that we have not reached our goal
and those principles have let us physicists down.
Note,
although the above is a non relativistic version of CED, the CED story
is truly relativistic and gauge invariant and it serves as a model to
many further theory developments. In particular, nowadays in QFT they
"derive" the wrong self-action Lagrangian from a "principle of local
gauge invariance" (a gauge principle for short). They find it beautiful
mathematically, enjoy the equation symmetries and conservation laws that
follow from this symmetry. They repeat QED where they think there is
this "gauge principle". However such gauge equations do not have
physical solutions, so their conserved quantities are just a bullshit.
During enjoying the beauty of gauge interaction, they omit to mention
that the solutions are non physical. The gauge principle in QED does not
lead to physical equations. We are forced to rebuild a gauge theory, as I outlined above. In CED the
bare and electromagnetic masses appear and disappear shortly after, but
in QED and QFT they are present in each perturbative order. In
addition, the physical charge also acquires unnecessary and bad
"corrections", and their omnipresence makes an impression of their
belonging to physics.
Next,
new "principles" come into play - they come into play with the purpose
to fix this shit. Those principles serve to "allow" multiple replacements of
bad terms in solutions with better ones - it's bare stuff and
renormalizations, of course. A whole "fairy science" about a "vacuum polarization" around a still
"bare" charge is developed to get rid of bad perturbative corrections in
this wrong gauge construction (renormalization group). It boils down to adding a counter-term
Lagrangian $ \mathcal{L}_{CT}$ to the gauge one $ j\cdot A$:
$ \mathcal{L}_{int}^R =j\cdot A+\mathcal{L}_{CT},\qquad (8)$
so the interaction becomes different from a purely gauge one. (Often it is presented as imposing physical conditions to a (bad) theory.) Thus, the bare stuff and bad corrections cancel each other and do not exits any more. That's their fate - to disappear from physics forever,
if you understand it right. And it is we who make them disappear, not
physical phenomena like vacuum polarization, etc. In other words,
renormalization is not a calculation, but a specific modification of
calculation results.
But
this fix is not sufficient either. They need to sum up soft diagrams
too (to all orders) in order to obtain physically meaningful results
because, alas, the electron does not correctly radiate otherwise and
calculation fails! The latter fact shows eloquently that some part of
"perturbation" (8) (let's call it figuratively $ \mathcal{L}_{soft}$) is not
small and should be taken into account exactly (joined with $ \mathcal{L}_0$,
hence, removed from the "perturbation"):
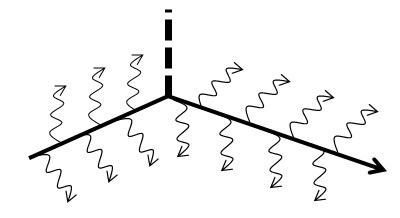
Fig. 3. Electron scattering from an external field in the first Born approximation, as it must be.
$ \tilde{\mathcal{L}}_0=\mathcal{L}_0+\mathcal{L}_{soft},\qquad (9)$
$ \tilde{\mathcal{L}}_{int}^R =j\cdot A+\mathcal{L}_{CT}-\mathcal{L}_{soft}.\qquad (10)$
Such
taking into account exactly is in fact using another, more physical,
zeroth-order approximation with Lagrangian $ \tilde{L}_0$ (9). The
electron charge $ e$ is involved there non perturbatively, so the
electron is already coupled with the field variables, at least,
partially (I call such an approximation an "electronium" [5]).
Interaction (10) is even more different from the "gauge" one. (A good qualitative and quantitative analogy to such IR-divergent series
and their exact sums is the second atomic form-factor $f_n ^n
(\mathbf{q})$ (3) and its series in powers of $m_e/M_A$ when
$ |\mathbf{q}|=const$ and $n\to\infty$, see Fig. (3) in [5] and Fig. 2, Fig. 3 in [6].)
You see, our former initial approximation (decoupled electron in $ \mathcal{L}_0$) is not physical. You know why? Because we admit free particles in our minds and thus in equations. We observe interacting macroscopic bodies. In the simplest case we speak of a probe body in an external force. Sometimes the external forces add up into nearly zero and they do not change noticeably the body kinetic energy. Then we say the probe body is "free". But we observe it with help of interactions too (inclusive image obtained with photons, for example), so it is never free, as a matter of fact, and, of course, its mass is not bare. For electron it also means that its very notion as a "point particle" and its equations is an inclusive picture of something compound [5]. An electron coupled within field oscillators has a natural mechanism of "radiation reaction" and a natural inclusive picture. Such a coupling is always on and never is off, unlike the gauge term $ j\cdot A$ treated perturbatively. W. Pauli always argued that one should look for a formulation of QED (or a field theory in general) which would mathematically not allow the description of a charged particle without its electromagnetic field. Now, seeing to what extent $ \mathcal{L}_0$ and $ j\cdot A$ are different from (9) and (10), I can safely say that they really do not understand what to start with in their "gauge theories". Even a physical solution of a partially coupled electron (a "hairy" electron line in Fig. 3) is not written, understood, and explained in QED, but who cares?
In
electroweak unification they wanted to make the weak part of
interaction to be a "gauge" too, but the gauge fields are massless. What
a pity! Not only this construction needs counter-terms and soft diagram
summations, now it needs a special "mechanism" to write down the mass
terms in $ \mathcal{L}_0$. Such a fix was found and it is known now as a
Higgs mechanism. This fix to a bad gauge interaction idea is presented
now as the ultimate explanation of the nature of mass: "Every ounce of mass found in the universe is made possible by the Higgs boson."
I wonder how were we doing before Higgs? With writing down
phenomenological mass terms, we were in error, weren't we? No. Then why
all these complications? Because they do not know how to write down interactions
with massive particles correctly (an old story, see (9) and (10)
above). All they write is not only non physical, but also non
renormalizable, so they decided to try here
the gauge principle too. Fortunately or unfortunately, some such constructions are
renormalizable, thus they survived.
We
remember the fiasco with the electron electromagnetic mass, and the
Higgs proper mass is not really different since the Higgs boson acquires
its own mass due to "self-action" too. It is not a calculation but a fake since the Higgs boson mass is taken from experiment.
The Standard Model is also furnished with "fine tuning mechanism" because otherwise it is still a bullshit. And let me mention fitting parameters coming with the "Higgs mechanism". Now the fitting properties of theory increased. Some, however, confuse it with increase of "predictive power".
The Standard Model is also furnished with "fine tuning mechanism" because otherwise it is still a bullshit. And let me mention fitting parameters coming with the "Higgs mechanism". Now the fitting properties of theory increased. Some, however, confuse it with increase of "predictive power".
To
me the Higgs is a fix, a fix somewhat similar to the bare mass term in
CED compensating an obviously wrong construction, but a more complicated
fix. I do not think it is an achievement. A bare mass notion is not an
achievement in physics. The freedom in choosing the cutoff $
\Lambda$ in a relationship $ m_0(\Lambda)=m_e-m_{em}(\Lambda)$ (à
la renorm-group) is not physics, $ \Lambda$-independence of $
m_e$ is not a CED "universality". I hope I am clear here. But nowadays
particle physics is stuffed with artefacts of our patches and stopgaps,
so it is really difficult to distinguish what is physical and what is a
fairy tale (a fake).
Today
they sell you the bare stuff, its self-action dictated with the gauge
principle, then counter-terms, IR diagram summation, Higgs field with
self-action and fine tuning, poisons and antidotes, shit with nutlets., etc. as a
physical theory. They are very pushy in that. They grasped all the principles of Nature.
No,
they fool themselves with "clever insights" and fairy tales instead of
doing physics. They count on "guiding principles", they are under the
spell of the gauge and other principles. Sticking to them is like being possessed. This fact underlines the shaky grounds the modern QFT is
based on.
No, the conceptual problems have not been resolved, let us recognize it. We must not dope ourselves with self-fooling and self-flattering.
(To be updated.)
[1] Laurie M. Brown (editor). Renormalization From Lorentz to Landau (and beyond), 1993, Springer-Verlag, the talk of Max Dresden.
[2] Kerson Huang, A Critical History of Renormalization, http://arxiv.org/abs/1310.5533
[3] H. Lorentz, Landau-Lifshitz, R. Feynman, etc.
[4] Fritz Rohrlich, The dynamics of a charged particle, (2008) http://arxiv.org/abs/0804.4614
[5] Vladimir Kalitvianski, Atom as a "Dressed" Nucleus, Central European Journal of Physics, V. 7, N. 1, pp. 1-11 (2009), http://arxiv.org/abs/0806.2635
[6] Vladimir Kalitvianski, On integrating out short-distance physics, http://arxiv.org/abs/1409.8326



Комментариев нет:
Отправить комментарий