Это фраза из выступления Дирака, сделанного им на конференции по квантовой хромодинамике в 1981 году. В докладе всего две страницы, а интересующие нас высказывания занимают и того меньше места. Там он четко говорит, что перенормировка есть рабочее правило, а не математическое вычисление. Он замечает, что многие физики вполне счастливы таким положением дел, раз есть согласие с экспериментом. Но этого, заявляет Дирак, не достаточно. Хотелось бы понять, как функционирует Природа. Золотые слова!
Дирак был смелым новатором в физике и даже в математике, а не отсталым недоумком, как некоторые стараются представить его в свете "успехов перенормировок". Дирак полагал успех перенормировок случайностью (а fluke, см. его лекцию после t=58:15), а я полагаю вреднейшей случайностью, дурманящей многие светлые умы. Не ведают они, как функционирует Природа.
Я уже раньше разбирал, как возникают поправки к константам, а здесь (и здесь) покажу совсем вкратце. Есть пара модельных экспериментальных уравнений, одно "механическое", а другое "волновое" (опубликовано в International Journal of Physics):
Глядя на второе уравнение, говорят, что ускорение частицы "создает" излучение. Заметьте, здесь ускорение 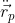 есть известная функция времени, некакая
есть известная функция времени, некакая ) , "внешняя" по отношению к волновому уравнению (2).
, "внешняя" по отношению к волновому уравнению (2).
Второе уравнение можно переписать через внешнюю силу:
Второе уравнение можно переписать через внешнюю силу:
Отсюда сразу видно, что дергая за частицу, мы дергаем осциллятор, то есть, частица есть неотъемлемая часть осциллятора и в этом содержится вся физика того, как функционирует Природа, но так почему-то никогда не рассуждают, а думают, что волны "отрываются" от частицы. В этом состоит физическая ошибка теоретиков. "Частица" и "осциллятор" являются нетривиальными "частями" сложной системы.
Механическое уравнение (1) вызывает неудовольствие тем, что в нем нет члена, учитывающего потери на возбуждение осциллятора. Я не буду здесь писать пробный "Лагранжиан взаимодействия", а скажу сразу, что правильный член "реакции излучения" есть 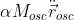 :
:
Возникает вопрос, с каким волновым уравнением надо использовать (4)? С тем, что записано через внешнюю силу, т.е. с (3)? Да, конечно, система (3)+(4) есть правильная система уравнений, но все пишут волновое уравнение (2) с ускорением в правой части (так как выбирают "Лагранжиан взаимодействия" 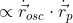 ) и не замечают совершаемой таким образом математической ошибки:
) и не замечают совершаемой таким образом математической ошибки:
Действительно, здесь достаточно выразить ускорение 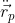 через внешнюю силу и силу реакции излучения, подставить его в волновое уравнение, и сразу выясняется, что волновое уравнение стало другим:
через внешнюю силу и силу реакции излучения, подставить его в волновое уравнение, и сразу выясняется, что волновое уравнение стало другим:
или
Собственная частота осциллятора изменилась и константа связи тоже, что, конечно, плохо, поскольку решение перестает соответствовать экспериментам. Этого не планировалось и это надо исправлять. (На самом деле в стандартном члене "реакции излучения" КЭД содержится еще и "поправка" к массе частицы за счет дополнительного члена 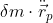 , так что и кинетический член механического уравнения меняется тоже, но здесь я опускаю эту деталь ради простоты). Так получилось потому, что вместо известной функции времени
, так что и кинетический член механического уравнения меняется тоже, но здесь я опускаю эту деталь ради простоты). Так получилось потому, что вместо известной функции времени ) в правую часть осциллятора подставили неизвестную искомую переменную
в правую часть осциллятора подставили неизвестную искомую переменную 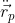 , связанную с
, связанную с 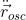 через новое механическое уравнение. Вот куда завел этот пробный Лагранжиан взаимодействия.
через новое механическое уравнение. Вот куда завел этот пробный Лагранжиан взаимодействия.
Возврат к прежним константам достигается невозмутимым использованием старых численных значений для "новых" констант 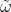 и
и 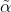 в (9). Говорят себе и другим, мол, наша теория (9) ведь должна описывать эксперимент и поэтому используют старые, проверенные числа. Так функционирует, конечно, человек, а не Природа. Это "использование" эквивалентно отбрасыванию "поправок" к старым константам в (10) и называется перенормировкой констант. Про это-то и толковал Дирак, что это не расчет, а рабочее правило. Заметьте, перенормированные уравнения совпадают с правильной системой (3), (4). Вот оно, везение. Испорченное уравнение (9) оказалось таким же по форме, как и правильное (3), и исправление испорченного осуществляется простой перенормировкой констант. Так стоит ли городить всю эту лженауку о затравочных частицах и поляризации вакуума, если все это неправда, если испорченное уравнение (9) есть просто позорный плод наших творческих усилий, а не физическая реальность, и если правильное физическое решение находится у нас в руках прямо в (3) с (4)? Можно показать, что перенормировки эквивалентны вычитанию из старого "Лагранжиана взаимодействия" контрчленов и перегруппировке членов полученного Лагранжиана, то есть, признанию ошибочности исходного пробного Лагранжиана взаимодействия.
в (9). Говорят себе и другим, мол, наша теория (9) ведь должна описывать эксперимент и поэтому используют старые, проверенные числа. Так функционирует, конечно, человек, а не Природа. Это "использование" эквивалентно отбрасыванию "поправок" к старым константам в (10) и называется перенормировкой констант. Про это-то и толковал Дирак, что это не расчет, а рабочее правило. Заметьте, перенормированные уравнения совпадают с правильной системой (3), (4). Вот оно, везение. Испорченное уравнение (9) оказалось таким же по форме, как и правильное (3), и исправление испорченного осуществляется простой перенормировкой констант. Так стоит ли городить всю эту лженауку о затравочных частицах и поляризации вакуума, если все это неправда, если испорченное уравнение (9) есть просто позорный плод наших творческих усилий, а не физическая реальность, и если правильное физическое решение находится у нас в руках прямо в (3) с (4)? Можно показать, что перенормировки эквивалентны вычитанию из старого "Лагранжиана взаимодействия" контрчленов и перегруппировке членов полученного Лагранжиана, то есть, признанию ошибочности исходного пробного Лагранжиана взаимодействия.
Короче, я хотел показать, что можно элементарно ошибиться при написании новых, иначе связанных уравнений, не будем этого исключать. Но люди упрямо стоят на старом Лагранжиане взаимодействия и с умным видом делают перенормировки, а ошибку моделирования не признают. Не видят и не хотят видеть ошибки. Это так по человечески! Так функционирует природа слабого человека.
Раз на то пошло, то уравнения (1) и (2) уже в значительной степени физичны и точны, так как уравнение для координаты центра масс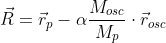 сложной системы совпадает с (1) в случае однородной внешней силы. Собственно, экспериментально часто наблюдается как раз движение центра масс
сложной системы совпадает с (1) в случае однородной внешней силы. Собственно, экспериментально часто наблюдается как раз движение центра масс  - в случае слабо-неоднородной внешней силы осцилляции
- в случае слабо-неоднородной внешней силы осцилляции  и
и 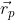 усредняются за счет конечной "выдержки" при наблюдении:
усредняются за счет конечной "выдержки" при наблюдении: 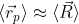 , так что (1), как феноменологическое уравнение, правильнее относить к центру масс системы
, так что (1), как феноменологическое уравнение, правильнее относить к центру масс системы  , а не к самой частице, на которую действует внешняя сила. Тогда переход к точным (не усредненным) уравнениям осуществляется "удлиннением" аргумента внешней силы в (1) и (2) (
, а не к самой частице, на которую действует внешняя сила. Тогда переход к точным (не усредненным) уравнениям осуществляется "удлиннением" аргумента внешней силы в (1) и (2) (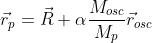 ):
):
\qquad(11))
Короче, я хотел показать, что можно элементарно ошибиться при написании новых, иначе связанных уравнений, не будем этого исключать. Но люди упрямо стоят на старом Лагранжиане взаимодействия и с умным видом делают перенормировки, а ошибку моделирования не признают. Не видят и не хотят видеть ошибки. Это так по человечески! Так функционирует природа слабого человека.
Раз на то пошло, то уравнения (1) и (2) уже в значительной степени физичны и точны, так как уравнение для координаты центра масс
Последнее уравнение можно переписать "через ускорение" в правой части:
что очень напоминает второе уравнение, выписанние в самом начале заметки.
Для небольшого количества колебаний отличие среднего значения координаты частицы от координаты центра масс ничтожно, поэтому уравнение (1) хорошо работает для ограниченного интервала времени. Лишь при очень длительном периоде наблюдения систематическое отклонение частицы от положения центра масс может стать заметным из-за систематической накачки колебаний осциллятора (
например, при вращении электрона в однородном магнитном поле.

Комментариев нет:
Отправить комментарий