Интеграл от квадрата дельта-функции равен бесконечности, как ни крути: подынтегральное выражение сугубо положительное и большое - еще больше, чем сама дельта-функция, так что никакой двусмысленности тут нет.
А бывает, очень хочется, чтобы этот интеграл был равен нулю. Не потому, что есть сомнения в его значении, а просто если он равен нулю, то расчет в теории получается конечным и сравнимым с экспериментальными данными, вместо бесконечного и никуда не годного ответа. Можно приравнять сугубо положительное число нулю, если этого "требует" эксперимент. Вот она, истинная мотивация, а не какая-то там высшая математика. Это - интеллектуальная вершина теоретической физики и краеугольный камень всех успехов. Если нельзя, но очень хочется, то можно!
Возьмем, например, и рассчитаем наименьшее собственное значение в двухслойной задаче Штурма-Лиувилля (формулы (1-8) в [1]):
$\lambda_0 \approx \lambda_0^{(0)} + U_{00}$ (1)
$U_{00} = \int \Phi_0^{(0)}U(z) \Phi_0^{(0)}dz = \Phi_0^{(0)} (z_1) \Phi_0^{(0)} ' (z_1)\ln\sqrt {r_1/r_2} - \frac{1}{16} \int [\ln \sqrt{r}]'^2 {\Phi_0 ^{(0)}}^2 dz $ (2)
Первое слагаемое в матричном элементе конечно, а второе бесконечно, если от слоя к слою коэффициент $r(z)$ изменяется скачкообразно (штрих, разумеется, означает производную). При этом трансцендентное уравнение для $\lambda_0$:
$e^{\ln\sqrt {r_1/r_2}} ctg(\sqrt{\lambda}z_1) = tg[\sqrt{\lambda}(1-z_1)] (3)
само по себе вполне разумно: оно имеет разложение по степеням логарифма $\ln\sqrt {r_1/r_2}$ и не содержащее никаких расходящихся членов. В частности, согласно (3), первая поправка к наименьшему собственному значению есть $\Phi_0^{(0)} (z_1) \Phi_0^{(0)} ' (z_1) \ln\sqrt {r_1/r_2}$, т.е., первое слагаемое из (2). Вообще двухслойная задача всегда имеет конечные точные решения; просто характеристическое уравнение для собственных значений получается трансцендентным, неразрешимым точно относительно $\lambda$, но его всегда можно разложить в ряд Тейлора и сравнить с рядом из теории возмущений. И вот оказывается, что члены ряда Тейлора для (3) все конечны и разумны, в отличии от матричных элементов, содержащих бесконечности.
Такая ситуация сродни ситуации в физике высоких энергий - на эксперименте все конечно, разумно, а в расчетах - полно бесконечностей. Однако наша ситуация [1] лучше - мы всегда можем получить аналитическое разложение в ряд Тейлора из уравнения (3) без привлечения теории возмущений, тогда как в физике высоких энергий нет другого способа делать расчеты, кроме как по теории возмущений.
Короче, вот вам дилемма, как все-таки "делать расчеты" по теории возмущений, зная, что точные решения существуют и заведомо конечны, а матричные элементы содержат расходящиеся интегралы? Такова была реальная ситуация, с которой столкнулся и я тридцать лет назад.
Нужно иметь ввиду, что я знал о перенормировках больше, чем нам тогда преподавали. Я самостоятельно читал разные книжки на эту тему, включая монографии Боголюбова и Ширкова. Я хорошо помнил две мотивации перенормировок - обычную, проводимую в импульсном пространстве, и Боголюбовскую, которая оперирует с обобщенными функциям в координатном пространстве. Почему я интересовался этим - скажу: хотелось по-строже понять физический смысл перенормировок. Откуда в теории берутся бесконечности и как их победить с чистой совестью. И поскольку не только меня одного мучила совесть, но и многих моих предшественников и современников, то я и почитывал разную литературку - мнения опытных людей на эту тему. Это же важно, чувствовать физику за той или иной техникой вычислений. Разумеется, в подробности я не входил, в смысле, сам вычисления не повторял, а верил книжкам на слово. И каждая книжка по своему толковала возникающие трудности.
Из книжки Боголюбова я помнил, что, раз произведение обобщенных функций не определено, то его можно доопределить так, чтобы получить конечные матричные элементы. Тогда это было наиболее убедительно для моего молодого ума. Ведь в самом деле, раз так получается в теории, что матричные элементы выражаются в виде интегралов от произведения обобщенных функций (colliding infinities), а решение должно быть конечным ;-), то мы ну просто обязаны обосновать такое вычисление (вычитание контр-членов), чтобы получить конечный ответ. В КТП это обоснование производится путем сравнения с экспериментом - ведь теория должна описывать эксперимент. Логично!
Вот с таким настроем я и таращился на мой интеграл от квадрата дельта-функции в (2) в 1981-82 годах. И если в (2) этот интеграл можно было просто отбросить, то в недиагональных матричных элементах нужно было отбрасывать некоторую более сложную комбинацию, для чего требовалось более солидное обоснование. Короче, нужно было придумать, как приписать интегралу от квадрата дельта-функции "нужное" значение и как его обосновать. И скажу честно, было одно мгновение, когда я, подражая великим, искренне подумывал напустить туману и "определить" значение чисто математического интеграла из "экспериментальных данных". Но даже тогда, когда я еще не знал правильного решения, такой сценарий "вычислений" вызывал у меня кривую улыбку - уж больно искусственным казалось приписывание какого попало значения чисто математическому выражению. Ну а что, если экспериментатор ошибется, или произойдет недоразумение между экспериментатором и теоретиком, например, спутают на радостях единицы измерения? Неужели однозначное математическое выражение может так сильно зависеть от внешних случайных факторов? Или может быть оно не совсем математическое? А тогда что это?
Черная магия с полным ее разоблачением
А тогда это нематематическое и нефизическое поведение исследователя, идущего вразрез с элементарной математикой и логикой физических расчетов. Это поведение, чтобы получить "нужный" результат любой ценой. И пока результат не был известен экспериментально, люди еще сомневались в перенормировках, говорили о неоднозначности и вообще о невозможности приписывания одному числу другого значения. Но потом постепенно сдались. Не все, конечно, но многие позорно сдались. Спрятались за бесконечностью, как за такой "неопределенностью", которую "можно" делать определенностью, и положились на удачу всей затеи. Ведь мы знаем заранее, что в конце будет удача! Вот если бы явно конечному числу пришлось бы приписывать нулевое значение, то тогда да, так было бы нельзя, а бесконечности - можно.
Пардон, но регуляризованное выражение конечно и сугубо положительно! Это как раз тот случай! Как раз тот случай! Это-то и смущало всех без исключения основателей квантовой механики и квантовой электродинамики - приписывание одному числу другого значения. И меня это смущало до невозможности, и я разобрался все-таки, в чем тут дело.
И вправду, взгляни, читатель, на интеграл: $\int [\ln \sqrt{r}]'^2 {\Phi_0^{(0)}}^2 dz $. Ну какой же он ноль, если он - большое и положительное число? Нуля я так и не смог принять и усомнился в авторитетах. Честно скажу - меня за это до сих пор бьют и авторитеты, и те, кто в них не сомневается, хотя рисунок под заголовком этой заметки демонстрирует их неправоту $(a\gg 1)$ .
А ларчик просто открывался: начальное приближение для собственных функций оказалось слишком далеким от точного решения и пертурбативные поправки получились большими именно для того, чтобы исправлять изначально сильный перекос. Так бывает и с аналитическими итерациями, и с численными. Аналитически в нашем примере это означает подставлять в разложение Тейлора-Маклорена некой функции $f(x)$ очень большое значение $ x $ - все члены, кроме нулевого приближения, расходятся. Вот если бы учесть такую функцию точно ($f(\infty)=const$), то остальное дало бы нормальный ряд. Таким образом, все дело в исходных уравнениях и в качестве начального приближения, используемого для итераций. Стоит выбрать лучшее приближение, как жизнь сразу налаживается. Очень понятно и очень математично. К сожалению, исследователи в КТП чрезмерно полагаются на уравнения и начальные приближения, считая их правильными. Ведь уравнения такие красивые, а мы такие умные. Мы никак не можем ошибаться, а это просто затравочные частицы гадят, гады! И давай аксиоматизировать ущербную модель ради получения после перенормировок случайно удачного результата. Валим вину на матушку природу и восхваляем себя, тогда как это чисто наши человеческие просчеты моделирования.
А ларчик просто открывался: начальное приближение для собственных функций оказалось слишком далеким от точного решения и пертурбативные поправки получились большими именно для того, чтобы исправлять изначально сильный перекос. Так бывает и с аналитическими итерациями, и с численными. Аналитически в нашем примере это означает подставлять в разложение Тейлора-Маклорена некой функции $f(x)$ очень большое значение $ x $ - все члены, кроме нулевого приближения, расходятся. Вот если бы учесть такую функцию точно ($f(\infty)=const$), то остальное дало бы нормальный ряд. Таким образом, все дело в исходных уравнениях и в качестве начального приближения, используемого для итераций. Стоит выбрать лучшее приближение, как жизнь сразу налаживается. Очень понятно и очень математично. К сожалению, исследователи в КТП чрезмерно полагаются на уравнения и начальные приближения, считая их правильными. Ведь уравнения такие красивые, а мы такие умные. Мы никак не можем ошибаться, а это просто затравочные частицы гадят, гады! И давай аксиоматизировать ущербную модель ради получения после перенормировок случайно удачного результата. Валим вину на матушку природу и восхваляем себя, тогда как это чисто наши человеческие просчеты моделирования.
Да, мы можем ошибаться, не будем это отрицать. И можем исправляться, если захотим. Не все, однако, хотят и не все понимают. Да и трудно расставаться с любимой замусоленной игрушкой, к которой так привык и которая тешит самолюбие. Наконец, все же делают перенормировки! Зачем же что-то менять? Не нравится одно "объяснение" перенормировок, подбери другое, которое больше по душе. Г. Шарф, например, уверяет, что расходимостей и перенормировок вообще нет - интеграл ноль, так как аргументы у дельта-функций в произведении $\delta (x - x_0)^2 = \delta (x - x_0) \cdot \delta (x - x_0)$ не совпадают! Оригинально? Безусловно! А правильно? Г. Шарф считает, что правильней, чем у Боголюбова. Боголюбов для подгонки под эксперимент делает вычитание (добавляет контр-члены), что кажется искусственным, а у Шарфа интеграл сам обращается в ноль, без вычитаний. Аргументы у дельта-функций не совпадают по причине причинности. Шарф не использует дифференциальные уравнения и начальные данные по причине их недостаточной причинности. Шарф берет и "применяет" условие причинности к самому интегралу. Во как! Поэтому ноль Шарфа, по мнению Шарфа, правильней и строже нуля строгого Боголюбова или, там, совсем не строгого нуля весельчака Фейнмана. Короче, Шарф, шельмец, строит аксиоматическую КЭД путем постулирования нужного ему и известного ему проверенного результата, а не уравнений.
Да, такая аргументация вполне понятна по-человечески - очень хочется нуля. Но это - не математическое обоснование, а обычная человеческая фигня, что и требовалось доказать. Самообман и опиум ученого народа. Можно и нужно сделать все лучше и правильней. Мне же удалось переформулировать задачу Штурма-Лиувилля. Неужели это плохой пример для извлечения уроков?
Жаль, конечно, что я так обессилел и не могу собраться, чтобы предоставить что-то завершенное. Рассчитываю в основном на пробуждение интереса к этой теме у других, молодых и энергичных исследователей. Правда таких очень и очень трудно найти. Как говорил Швингер: "Товарищ, ну где же ты?" ("I continue to hope that it has great appeal to the true physicist (Where are you?).", страница 420 в тексте = 441 в редакторе djvu).
Да, такая аргументация вполне понятна по-человечески - очень хочется нуля. Но это - не математическое обоснование, а обычная человеческая фигня, что и требовалось доказать. Самообман и опиум ученого народа. Можно и нужно сделать все лучше и правильней. Мне же удалось переформулировать задачу Штурма-Лиувилля. Неужели это плохой пример для извлечения уроков?
Итак, нет никакой такой уж неопределенности с расходящимися матричными элементами - они правильно расходятся и однозначно свидетельствуют о наших просчетах в физической модели. Исходная физическая модель содержит все определения и не нуждается в доопределениях на ходу и тем более после вычислений. Всякое другое толкование - от лукавого. И случайная удача перенормировок (отбрасываний) имеет свое объяснение, также как и закономерная неудача неперенормируемых теорий. Так что эксперимент вовсе не требует, чтобы интеграл $\int [\ln \sqrt{r}]'^2 {\Phi_0^{(0)}}^2 dz$ был равен нулю. Он требует такую теорию, в которой расходящихся интегралов в расчетах просто не возникает. Он требует переформулировки теории, a не исправлений (подгонки) негодных решений на ходу. Когда я это осознал, я стал искать в КЭД пороки начального приближения, ведь теперь они должны были бросаться в глаза. Они и вправду бросаются в глаза, и это очень обнадеживает. В первом неисчезающем приближении рассеяние зарядов "происходит" без излучения, которое в эксперименте происходит всегда. Это очень большая промашка для теории, претендующей на точнейшее описание вероятностей процессов.
Но не все, к сожалению, хотят это видеть или признавать и упорно продолжают рассчитывать действие частицы самой на себя, которое никому на свете не нужно (дельта-функция в квадрате под интегралом) и от которого потом всячески избавляются (считают, что это ноль без палочки) и заодно раскладывают с умным видом $f(x)=\frac{1}{(1+x)^2}$ в ряд Тейлора-Маклорена $f(x)=f(0)+f'(0)\cdot x+...$, когда численное-то значение $x$ равно бесконечности (инфракрасная катастрофа). Срамота да и только. Однако, я тоже не подарок. Прорвемся. Не такое исправляли.
Но не все, к сожалению, хотят это видеть или признавать и упорно продолжают рассчитывать действие частицы самой на себя, которое никому на свете не нужно (дельта-функция в квадрате под интегралом) и от которого потом всячески избавляются (считают, что это ноль без палочки) и заодно раскладывают с умным видом $f(x)=\frac{1}{(1+x)^2}$ в ряд Тейлора-Маклорена $f(x)=f(0)+f'(0)\cdot x+...$, когда численное-то значение $x$ равно бесконечности (инфракрасная катастрофа). Срамота да и только. Однако, я тоже не подарок. Прорвемся. Не такое исправляли.
Жаль, конечно, что я так обессилел и не могу собраться, чтобы предоставить что-то завершенное. Рассчитываю в основном на пробуждение интереса к этой теме у других, молодых и энергичных исследователей. Правда таких очень и очень трудно найти. Как говорил Швингер: "Товарищ, ну где же ты?" ("I continue to hope that it has great appeal to the true physicist (Where are you?).", страница 420 в тексте = 441 в редакторе djvu).

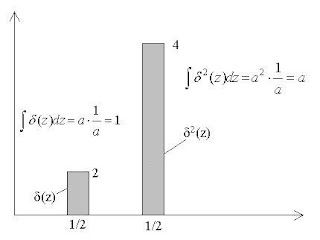
Очень хороший и наглядный график для дельтаобразных последовательностей.
ОтветитьУдалить